243 years later, quantum entanglement solves “impossible” problem

More than 240 years ago, the famous mathematician Euler raised a question: If each of the six legions has six officers with six different ranks, can they be arranged in a square formation so that the rows or columns do not repeat ranks or regiments?

After searching in vain for a solution, Euler declared the problem impossible, and more than a century later, French mathematician Gaston Tarry proved him right.Then, 60 years later Thatwhen the advent of computers eliminated the need to laboriously test every possible combination by hand, mathematicians Park, Bose, and Schlihand demonstrated an even stronger result: six times six squared was not only impossible, and it is only There is no solution at all for the size of the square other than two by two.

Now, in mathematics, once a theorem is proven, it is proven forever. So you might be surprised to learn that a 2022 paper published in the journal Physical Review Letters has apparently found a solution. There’s just one problem: The officer must be quantumly entangled.

“I think their paper is very beautiful,” quantum physicist Gemma De las Cuevas, who was not involved in the work, told Quanta magazine at the time. There’s a lot of quantum magic out there.Not only that, you can feel it throughout the paper [the authors] A love of problems.

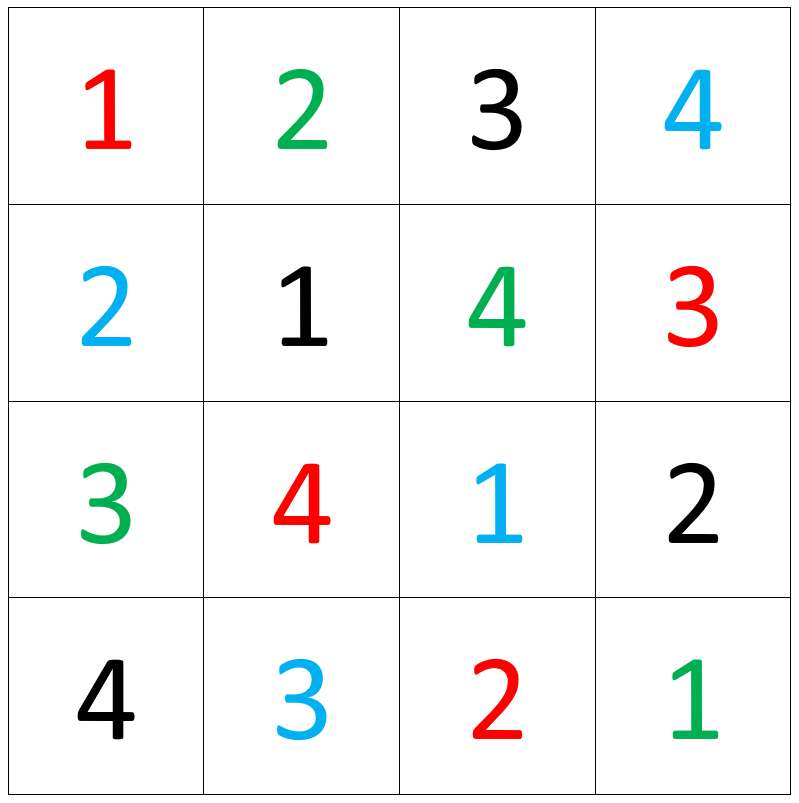
To explain what’s going on, let’s start with a classic example. As we all know, Euler’s 36 Officer problem is a special type of magic square called an orthogonal Latin square, which can be thought of as two Sudokus that must be solved simultaneously on the same grid. For example, a four-by-four orthogonal Latin square might look like this:

Since each square in the grid is defined by a fixed number and a fixed color, Euler’s original six-by-six problem is impossible.In the quantum world, however, things are more flexible: things exist in Overlay s country.

In basic terms, or at least, when we’re talking about quantum physics, this means that any given general can hold multiple ranks in multiple legions at the same time. Using our Colored Double Sudoku example, we can imagine a square in the grid filled with overlays of green twos and red ones.

Now, researchers believe there is a solution to Euler’s problem. But what is that?

At first glance, it looks like the team is making their job more difficult. Not only do they have to solve a six-by-six double Sudoku that was impossible in the classic setting, but now they have to do it in multiple dimensions at the same time.

Fortunately, though, they had something: first, a classical approximate solution they could use as a starting point, and second, the seemingly mysterious properties of quantum entanglement.

Simply put, two states are said to be entangled when one tells you something about the other. As a classic analogy, suppose you know that your friend has two children of the same gender, A and B (your friend is bad at naming). This means that knowing that child A is a girl can definitely tell you that child B is also a girl, and the genders of the two children are intertwined.

Entanglement doesn’t always work well with this problem, where one state can tell you everything about the other, but when it happens, it’s called an absolutely maximally entangled (AME) state. Another example might be a coin toss: if Alice and Bob each toss a coin, and Alice lands heads, then if the coins are tangled, Bob knows he lands heads without having to look, and vice versa.

It’s worth noting that the solution to the quantum officer problem was shown to have this property, and that’s what makes it really interesting. See, the above example works for two coins, three coins, but for four coins, this is not possible. But the 36-officer problem is not like rolling a dice, the author realizes, it is more like rolling entangled dice.

[Imagine that] Alice chooses any two dice and rolls them to obtain one of 36 equally possible outcomes, while Bob rolls the remaining outcomes. The paper explains that if the entire state is AME, then Alice can always deduce the result obtained by Bob’s part of the four-party system.

Furthermore, the authors continue, this state allows one to transport any unknown quantum state of two dice from any two owners of the two subsystems to a laboratory that possesses the entangled state of the other two dice of the quadrilateral system. This is not possible if the dice are replaced with two-sided coins.

Because these AME systems can generally be explained in terms of orthogonal Latin squares, researchers have known that they exist for four people to roll dice with any number of sides, that is, except for two or six sides. Remember: those orthogonal Latin squares don’t exist, so they can’t be used to prove the existence of AME states in that dimension.

However, by finding a solution to Euler’s 243-year-old problem, researchers did something surprising: they discovered a six-dimensional, square AME system. By doing so, they might even discover an entirely new AME that has no analogue in the classic system.

Euler claimed in 1779 that there is no solution. The author writes that Tarry’s proof came just 121 years later, in 1900. Another 121 years passed before we came up with a quantum version of the solution in which officers could be entangled.

They conclude that the quantum designs presented here may spark further research in the emerging field of quantum combinatorics.

The research was published in Physical Review Letters.

An earlier version of this article was published in January 2022.